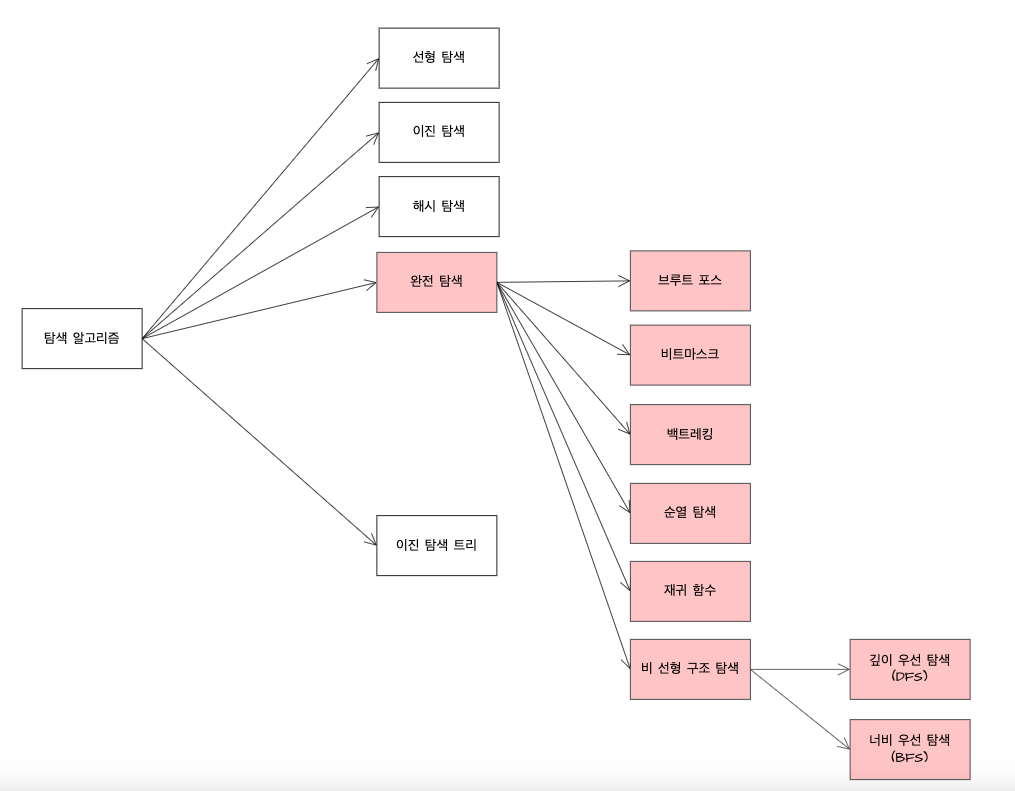
완전탐색❓
완전탐색은 알고리즘 패러다임중 하나로 가능한 모든 해를 찾아내어 그 중 조건을 만족하는 최적해를 찾아내는 방법이다. 완전탐색은 모든 가능성을 확인하기때문에 가장 정확하고 최적의 해를 구할 수 있지만, 시간복잡도가 매우 높아질 수 있다.
예를 들어, 4자리의 암호로 구성된 자물쇠를 풀려고 시도한다고 생각해보자. 이 자물쇠가 고장난 것이 아니라면, 반드시 해결할 수 있는 가장 확실한 방법은 0000 ~ 9999까지 모두 시도해보는 것이다.(최대 10,000번의 시도로 해결 가능)
모든 문제에 대해 완전탐색을 적용시키면 항상 답은 구해지겠지만 코딩테스트가 제한하는 시간안에 문제를 해결하지 못 할 가능성이 크다. 그렇기에 완전탐색을 사용해야 할 시점은 다음과 같다.
1. 주어진 입력의 범위가 작아 가능한 모든 해를 찾는 시간이 적게 들 때 즉, 시간 복잡도를 계산하고 될 거 같다 싶으면 일일이 다 하면 된다. 반복문이 몇 개든, 비효율적인 풀이 같아 보여도 상관없이 풀이를 작성해나가면 된다.
2. 코딩 테스트의 문제는 대체로 시간 복잡도가 10^8이내인 경우 통과가 된다. 그렇기에 입력의 범위가 100과 같이 작은 경우 완전 탐색으로 걸리는 시간 복잡도가 O(n^2)이라면 해당 방법은 10^4의 시간 복잡도를 갖기에 통과가 될 것이다. 이와 같이 주어진 입력의 범위가 작아 완전 탐색의 시간 복잡도 또한 낮아지는 경우 완전 탐색으로 빠르게 구현하여 문제를 해결할 수 있다.
3. 우선적으로 완전탐색으로 답을 구하고 그 과정을 최적화하여 시간을 줄이고 싶을 때
- 정렬
- 메모이제이션
- 투포인터
- DP
- 백트래킹
- 이진탐색
4. 주어진 입력의 범위가 커서 완전 탐색으로는 시간제한을 맞추지 못하는 문제에도 우선 완전 탐색을 적용시키는 방법을 고려할 수 있다. 완전 탐색은 앞서 설명했듯이 문제를 푸는 가장 기초적인 방법이다. 그렇기에 완전 탐색을 우선 구현한 후 해당 방법을 개선해 나감으로써 시간제한을 맞출 수 있다. 또한 완전 탐색을 통해 진행되는 문제의 과정을 보고 문제의 유형을 파악할 수 있는 등 문제의 명확한 풀이 방법을 찾지 못했을 경우에는 우선 완전 탐색으로 구현하는 것도 좋은 방법이다.
❔ 완전 탐색 vs 브루트 포스
위 완전 탐색과 브루트 포스는 종종 혼용되어 사용하는데 차이는 존재한다. 두 패러다임 모두 가능한 모든 해를 찾아내는 것은 같지만, 완전 탐색은 그 모든 해를 찾아나가는 과정이 보다 체계적인 방면 브루트 포스는 모든 해를 찾아나가는 과정이 이름 그대로 무식(Brute) 하게 모든 해를 찾아나간다는 것이 패러다임의 차이다. 하지만 많은 강의에서 두 용어를 엄밀하게 구분하진 않는다.
❔선형 탐색 vs 완전 탐색
1차원 배열에서 최댓값 찾기같은 문제는 배열을 처음부터 끝까지 한 번씩 확인하면서 현재 최댓값을 갱신해나가는 문제인데 그렇다면 각 요소를 반드시 다 확인하니 이 문제 또한 완전 탐색 알고리즘에 속하는것이 아닌지 궁금해졌다. 결론부터 말하면 완전 탐색 알고리즘이 아닌 선형(순차) 탐색 알고리즘이다.
🔹 선형 탐색 (Linear Search)
- 특정 데이터 구조(대부분 1차원 배열)에서 앞에서부터 하나씩 확인해서 원하는 값을 찾는 단순한 탐색 방법이다.
- 보통 O(n) 시간 복잡도
- 목적: 어떤 값이 존재하는지 여부만 확인
🔹 완전 탐색 (Brute-force Search)
- 어떤 문제를 풀기 위해 가능한 모든 조합/경우의 수를 시도해보는 전략.
- 예: 순열, 조합, 부분집합, 백트래킹, 비트마스크 등
- 보통 O(2ⁿ), O(n!) 같은 매우 큰 시간복잡도를 가짐.
- 목적: 조건을 만족하는 최적의 해 또는 모든 해를 찾기 위함.
🔹 차이점
| 항목 | 선형 탐색 | 완전 탐색 |
| 탐색 목적 | 원하는 값(조건을 만족하는 값)이 있는지만 확인 | 최적의 해 또는 모든 해를 찾기 위함 |
| 종료 조건 | 원하는 값 발견 시 즉시 탐색 종료 가능 | 모든 경우를 시도해야 하므로 끝까지 수행해야 함 |
| 탐색 범위 | 단일 데이터 구조(배열 등)에서의 순차적 확인 | 가능한 모든 조합, 순열, 경로 등을 전부 확인 |
| 시간 복잡도 | O(n) | O(n!), O(2ⁿ), O(n^r) 등 다양하고 큼 |
| 전략 성격 | 단순 탐색 | 문제 해결을 위한 포괄적 전략 |
완전탐색 기법을 활용하는 방법❗
우선 완전탐색 기법으로 문제를 풀기 위해서는 다음과 같이 고려해서 수행한다.
1) 해결하고자 하는 문제의 가능한 경우의 수를 대략적으로 계산한다.
2) 가능한 모든 방법을 다 고려한다.
3) 실제 답을 구할 수 있는지 적용한다.
여기서 2)의 모든 방법에는 다음과 같은 방법 등이 있다.
- Brute Force 기법 - 반복 / 조건문을 활용해 모두 테스트하는 방법
- 순열(Permutation), 조합(Combination)
- 재귀 호출
- 비트마스크 - 2진수 표현 기법을 활용하는 방법
- BFS, DFS를 활용하는 방법
- 백트래킹
각 방식에 대한 설명✔️
① Brute Force 기법
이 방법은 반복 / 조건문을 통해 가능한 모든 방법을 단순히 찾는 경우를 의미한다. 예를 들어, 위의 자물쇠 암호를 찾는 경우와 같이 모든 경우를 다 참조하는 경우가 그러하다.
② 순열(Permutation), 조합(Combination)
순열은 서로 다른 n개 중에서 순서를 생각하며 r개를 택하는 경우의 수를 의미한다.
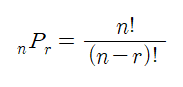
수식으로는 P(n, r) = n! / (n-r)!로 나타낼 수 있다. 전체 집합의 부분집합으로 볼 수 있는데 이로 인해 완전탐색 알고리즘 범주안에 있기도 하며, 시간복잡도는 O(n!)을 가진다.
// 순열 구현 코드
import java.util.Arrays;
public class Permutation {
static int count;
public static void main(String[] args) {
String[] stringArray = new String[]{"A", "B", "C"};
permutation(0, 2, 0, stringArray); // 두 번째 파라미터 값만 조정
System.out.println("총 갯수: " + count); // 총 갯수: 6
}
public static void permutation(int n, int r, int depth, String[] array) {
if(n >= array.length || depth >= r) {
System.out.println(Arrays.toString(Arrays.copyOf(array, r)));
count++;
return;
}
for(int a=n; a<array.length; a++) {
String temp = array[a];
array[a] = array[n];
array[n] = temp;
permutation(n+1, r, depth+1, array);
temp = array[a];
array[a] = array[n];
array[n] = temp;
}
}
}
순열 시간복잡도
컴퓨터에서 10의 8승은 굉장히 많은 것을 의미하고 있다. 언어에 따라 다를 수 있지만 기본적으로 컴퓨터의 10^8번 계산은 1초가 걸린다.
알고리즘 문제를 풀이할 때 입력 조건과 제한시간이 존재한다. 이때 입력 조건 n이 최대 범위가 100이라 하는 경우에 제한시간이 1초라면 대략 시간 복잡도 O(n^3) 풀이가 통과된다. (100*100*100=10^8)
다른 문제의 예시로 입력조건 n이 최대 범위가 10^8승이고 제한시간이 1초인 경우 시간 복잡도 O(n)의 풀이인 알고리즘을 선택해야 풀 수 있는 것이다.
입력 범위와 제한시간에 따라 선택 알고리즘이 달라진다는 것은 당연하게 받아들일 수 있지만,
10^8이 1초라는 사실에 입각하여 입력범위와 제한시간에 따라 가능한 시간복잡도를 알게 된다면 문제에 대한 알고리즘을 명확하게 선택할 수 있게 된다.
위에서 10^8이 무엇인지 알게 되었다면, 완전탐색 알고리즘이 가능한 문제를 알 수 있게 될 것이다. 완전탐색의 시간 복잡도의 경우 방법에 따라 다르기도 하지만 순열과 같이 오래 걸리는 경우는 O(2^n)과 O(n!)처럼 매우 오래 걸리는 경향이 있다.
하지만 1초는 10^8 임을 알고 있기 때문에 시간복잡도와 제한시간을 비교해 볼 수 있다. 입력조건의 최대범위를 시간복잡도 n에 대입하여 계산하여 제한시간과 비교할 수 있는 것이다.
이때 완전탐색의 시간복잡도가 제한시간 범위 안에 들어간다면, 완전탐색의 단점인 메모리와 시간이 오래 걸린다는 점은 무시한 채 쉬운 로직과 정확한 목푯값을 알 수 있는 장점을 활용할 수 있는 것이다.
순열의 경우의 수는 N!이므로 완전 탐색을 이용하기 위해서는 N이 한자리 수 정도는 되어야 한다.
N!은 굉장히 높은 시간 복잡도를 갖는다. N=10이면 되어도 약 360만 번의 연산이 수행되며 N=11이 되면 4억 번의 연산이 필요하다. 따라서 이 방법은 항상 사용할 수는 없고, 문제에서 주어진 N의 크기를 고려해야 한다.
✅ 순열이 완전 탐색인 이유
문제에서 “어떤 순서로 뭔가를 처리해야 하는 경우”, 예를 들어
- 여러 도시를 특정 순서로 방문할 때 (→ 여행 경로 문제)
- 숫자 카드를 순서대로 나열해서 조건에 맞는 경우를 찾을 때
- 특정 작업을 어떤 순서로 해야 할 때
이럴 때 모든 가능한 순서를 만들어보고, 그중에서 조건에 맞는 경우 즉, 정답을 찾는 방식은 완전 탐색이다.
예시①
[1, 2, 3]이라는 숫자가 있을 때, 이 세 숫자를 모두 사용해서 만들 수 있는 순열은
- [1, 2, 3]
- [1, 3, 2]
- [2, 1, 3]
- [2, 3, 1]
- [3, 1, 2]
- [3, 2, 1]
총 3! = 6가지 경우가 있다.
이건 세 수의 모든 순서를 다 만들어본 것, 즉 모든 경우의 수를 탐색한 것이니까 완전 탐색이다.
예시②
[1, 2, 3]이라는 숫자가 있을 때, 세 숫자 중 2개를 선택하여 숫자를 모든 순서대로 뽑는 경우의 순열은
- [1, 2]
- [1, 3]
- [2, 1]
- [2, 3]
- [3, 1]
- [3, 2]
순열 예제 - 가장 큰 두 자리 수 구하기
import java.util.*;
public class Permutation {
static int N = 4;
static int[] Nums = {1, 2, 3, 4};
static int solve(int cnt, int used, int val) {
if(cnt == 2) return val;
int ret = 0;
for(int i=0; i<N; ++i) {
if((used & 1 << i) != 0) continue;
ret = Math.max(ret, solve(cnt + 1, used | 1 << i, val * 10 +Nums[i]));
}
return ret;
}
public static void main(String[] args) {
System.out.println(solve(0, 0, 0));
}
}
// 출력:43
// 출처 : https://www.youtube.com/watch?v=CDLBg6wbhUQ
// 순열의 다른 구현 방법들 : https://define-me.tistory.com/178
조합이란 서로 다른 n개중에서 순서 상관 없이 r개를 선택하는 경우의 수를 의미한다. (순서 상관 없음)
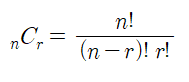
// 조합 구현 코드
public class Combination {
// 1. 백트래킹 구현
// 사용 예시 : combination(int[] arr, visited, 0, n, r)
static void combination(int[] arr, boolean[] visited, int start, int n, int r) {
if(r == 0) {
print(arr, visited, n);
return;
}
for(int i = start; i < n; i++) {
visited[i] = true;
combination(arr, visited, i + 1, n, r - 1);
visited[i] = false;
}
}
// 2. 재귀 사용
// 사용 예시 : comb(arr, visited, 0, n, r)
static void comb(int[] arr, boolean[] visited, int depth, int n, int r) {
if(r == 0) {
print(arr, visited, n);
return;
}
if(depth == n) {
return;
}
visited[depth] = true;
comb(arr, visited, depth + 1, n, r-1);
visited[depth] = false; // 빼먹지 않기!
comb(arr, visited, depth + 1, n, r);
}
public static void main(String[] args) {
int n = 4;
int[] arr = {1, 2, 3, 4};
boolean[] visited = new boolean[n];
for(int i = 1; i <= n; i++) {
System.out.println("\n" + n + "개 중에서" + i + "개 뽑기");
comb(arr, visited, 0, n, i);
}
for(int i = 1; i <= n; i++) {
System.out.println("\n" + n + "개 중에서" + i + "개 뽑기");
combination(arr, visited, 0, n, i);
}
}
// 배열 출력
static void print(int[] arr, boolean[] visited, int n) {
for (int i = 0; i < n; i++) {
if(visited[i]) {
System.out.print(arr[i] + " ");
}
}
System.out.println();
}
}
조합 예제 - 가장 큰 두 수의 합 구하기
import java.util.*;
public class Combination {
static int N = 4;
static int[] Nums = {1 ,2 ,3, 4};
static int solve(int pos, int cnt, int val) {
if(cnt == 2) return val;
if(pos == N) return -1;
int ret = 0;
ret = Math.max(ret, solve(pos + 1, cnt + 1, val + Nums[pos]));
ret = Math.max(ret, solve(pos +1, cnt, val));
return ret;
}
public static void main(String[] args) {
System.out.println(solve(0, 0, 0));
}
}
// 출력:7
// 출처 : https://www.youtube.com/watch?v=CDLBg6wbhUQ&t=40s
순열 조합 코딩테스트 문제
프로그래머스 순열 문제 - 피로도
백준 조합 문제 - 조합론
③ 재귀(Recursive)
재귀는 말 그대로 자기 자신을 호출한다는 의미이다. 왜 자기 자신을 호출할 필요가 있을까?
예를 들어, 총 4개의 숫자 중에 2개를 선택하는 경우를 모두 출력한다고 가정해보자. 1~4까지 숫자가 있고 2개를 중복 없이 선택하는 모든 경우의 수를 출력하고자 한다고 가정하자.
이를 반복문으로 표현한다면 다음과 같을 것이다.
public class Main {
public static void main(String[] args) {
for (int i = 1; i <= 4; i++) {
for (int j = i + 1; j <= 4; j++) {
System.out.println(i + " " + j);
}
}
}
}
// 출력
// 1 2
// 1 3
// 1 4
// 2 3
// 2 4
// 3 4손 쉽게 2중 반복문으로 해결하였다. 그런데.. 만약 숫자 N개의 숫자 중 M개를 고르는 경우라고 할 때, N과 M이 매우 큰 숫자라면 어떨까? 반복문을 수백, 수천 개를 써 내려갈 수는 없다!
이를 재귀 함수를 활용한다면 자기 자신을 호출함으로써 다음 숫자를 선택할 수 있도록 이동시켜 전체 코드를 매우 짧게 줄일 수 있다!
아래와 같이, 1~100의 숫자 중, 5개를 선택하는 경우를 코드로 작성해보자.
public class Main{
static int lim = 100; // 1~100까지의 제한
static int n = 5; // 5개만 고른다.
// chosen은 선택된 숫자가 저장된 배열
// curr은 현재 숫자를 선택하는 index
// cnt는 몇 개의 숫자가 선택되었는지 확인
private static void solve(int[] chosen, int curr, int cnt){
// n개의 숫자를 다 선택했다면 출력 후 더 이상 재귀를 돌지 않아야 한다!
// 탈출 조건의 정의!
if(cnt == n){
for(int i : chosen){
System.out.print(i + " ");
}
System.out.println();
return;
}
// 반복문을 통해 숫자를 계속 선택!
for(int i=curr+1; i <= lim; i++){
// 현재 선택된 숫자를 저장
chosen[cnt] = i;
// 다음 숫자를 선택하기 위해 재귀 호출
solve(chosen, curr, cnt+1);
}
}
public static void main(String[] args){
int[] chosen = new int[n]; // 선택된 숫자가 저장되는 배열
// 시작은 0부터 시작하며 0개를 현재 선택했으니 아래와 같이 parameter 전달!
solve(chosen, 0, 0);
}
}여기서 중요한 점!
⑴ 재귀를 탈출하기 위한 탈출 조건이 필요!
▶ 이것이 없으면 n개를 모두 골랐음에도 더 숫자를 선택하고자 하여 선택된 숫자를 저장하는 배열에 범위 초과 오류가 나거나, 다른 자료구조를 쓴 경우 잘못된 출력이 나올 수 있고, 혹은 무한 루프가 발생할 수 있다!
⑵ 현재 함수의 상태를 저장하는 Parameter가 필요!
▶ 위에서 우리는 curr, cnt를 통해 어떤 숫자까지 선택했는지, 몇 개를 선택했는지 전달하였다. 이것이 없다면 현재 함수의 상태를 저장할 수 없어 재귀 탈출 조건을 만들 수 없게 되거나 잘못된 결과를 출력하게 된다!
⑶ Return문을 신경 쓸 것!
▶ 위의 함수는 단순 출력이기에 void로 함수를 작성했다. 그런데, 재귀를 통해 이후의 연산 결과를 반환 후 이전 결과에 추가 연산을 수행하는 경우도 있을 수 있다. 즉, 문제 해결을 위한 정확한 정의를 수행하여야 이것을 완벽히 풀 수 있다.
잘 생각해보면 Dynamic Programming과도 매우 흡사해 보인다. 그 또한 Top-Down을 사용 시 재귀를 통해 수행하는데, 기저 사례를 통해 탈출 조건을 만들고, 현재 함수의 상태를 전달하는 Parameter를 전달한다.
또한 Return을 통해 필요한 값을 반환하여 정답을 구하는 연산 시에 사용하게 된다.
완전 탐색의 재귀와 DP의 차이점은, DP는 작은 문제가 큰 문제와 동일한 구조를 가져 큰 문제의 답을 구할 시에 작은 문제의 결과를 기억한 뒤 그대로 사용하여 수행 속도를 빠르게 한다는 것이다.
그에 반해 완전 탐색은 크고 작은 문제의 구조가 다를 수 있고, 이전 결과를 반드시 기억하는 것이 아니라 해결 가능한 방법을 모두 탐색한다는 차이가 있다.
(즉, DP는 일반적인 재귀 중 조건을 만족하는 경우에 적용 가능!)
④ 비트마스크(Bitmask)
비트마스크란 비트(bit) 연산을 통해서 부분 집합을 표현하는 방법을 의미한다.
비트 연산이란 다음과 같은 것들이 있다.
- AND 연산(&) : 둘 다 1이면 1
- OR 연산(|) : 둘 중 1개만 1이면 1
- NOT 연산(~) : 1이면 0, 0이면 1
- XOR 연산(^) : 둘의 관계가 다르면 1, 같으면 0
- Shift 연산(<<, >>) : A << B라고 한다면 A를 좌측으로 B 비트만큼 미는 것이다.
좀 더 쉽게 표로 알아보자. A, B라는 변수값이 있다고 할 때, 각각의 비트 연산결과를 표로 정리하였다.(Shift 연산은 아래에 별도로 정리함)
| A | B | A&B | A|B | ~A | A^B |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
그런데 우리는 1, 0만을 사용할 것이 아니라 각 모든 숫자를 비트 연산할 수 있어야 한다. 모든 숫자는 2진수로 표현될 수 있기 때문에 2진수를 통해 비트연산을 수행할 수 있다.
만약, 13과 72를 2진수로 나타낸다면 어떨까? 다음과 같을 것이다.
13 = 1101₍₂₎
72 = 1001000₍₂₎
그러면 13의 경우에는 부족한 앞의 3자리를 0으로 채우고 비트연산을 수행할 수 있다. 그 결과는 다음과 같다.
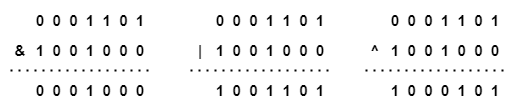
비트 연산의 시간복잡도는 내부적으로 상수 시간 정도로 처리가 되어 O(1)이라고 보면 된다.(그렇다고 프로그래밍 시 산술 연산을 비트 연산으로 모두 바꾸는 것은 오히려 비효율적. 유지보수에도 좋지 않고 실제로 미미한 차이만 나기 때문이다..)
NOT (^)연산 사용 시 주의할 점
코딩 시, 숫자들을 저장할 수 있는 자료형은 1가지가 아니다. Java의 경우 byte, short, int, long 형으로 정수 형태의 자료를 저장할 수 있다.
이 때, byte는 8비트, short는 16비트, int는 32비트, long은 64비트이기 때문에 전체 저장할 수 있는 비트의 수가 다르므로 어떤 자료형에서 NOT연산을 하느냐에 따라 숫자 자체의 결과는 같더라도 비트마스크 결과는 다를 수 있다.
예를 들어 40을 byte, short, int 형으로 저장한 뒤 각각을 NOT연산도 수행해보고, 비트 출력 또한 수행해보자.
public class Main{
public static void main(String[] args){
byte b = 40;
short s = 40;
int i = 40;
// byte, short는 toBinaryString이 없어 Integer클래스의 함수를 빌려와서 연산한다.
// 0xFF는 8비트로 11111111이므로 & 연산을 통해 결과를 나타낼 수 있다.
String bs = String.format("%8s", Integer.toBinaryString(~b & 0xFF));
System.out.println("Byte 형 40 NOT 연산 : " + ~b + ", 2진수 출력 : " + bs);
// 0xFFFF는 16비트로 1111111111111111이므로 & 연산을 통해 결과를 나타낼 수 있다.
String ss = String.format("%16s", Integer.toBinaryString(~s & 0xFFFF)).replace(' ', '0');
System.out.println("Short 형 40 NOT 연산 : " + ~s + ", 2진수 출력 : " + ss);
System.out.println("Integer 형 40 NOT 연산 : " + ~i + ", 2진수 출력 : " + Integer.toBinaryString(~i));
}
}
/* 결과
Byte 형 40 NOT 연산 : -41, 2진수 출력 : 11010111
Short 형 40 NOT 연산 : -41, 2진수 출력 : 1111111111010111
Integer 형 40 NOT 연산 : -41, 2진수 출력 : 11111111111111111111111111010111
*/위와 같이 숫자 자체는 같더라도 전체 비트 결과는 다르므로 주의해서 사용해야 한다. 만약 C++를 사용한다면 signed, unsigned 형까지 고려해서 연산을 수행해야 한다.
Shift 연산
그럼 Shift 연산에 대해서도 알아보자. <<, >> 로 표현하며 해당 방향으로 원 비트를 특정 값만큼 밀어버린다는 개념으로 이해하면 된다.
예를 들어서 1 << 3 이라고 한다면 어떨까? 1은 이진수로 1₍₂₎인데, 이를 3칸 좌측으로 밀어버리므로 1000₍₂₎가 된다.
그렇다면 7 << 3이라고 한다면 7000이 되나? 아니다. 7을 2진수로 변환한다음 3칸 밀어야 한다. 즉, 7은 이진수로 111₍₂₎ 이므로 3칸 좌측으로 밀면 111000₍₂₎가 된다.
반대로 >>는 우측으로 밀어버리는 것인데, 우측으로 밀어버리면 버려지는 것들은 어떻게 할까? 그냥 삭제되는 것이다. 예를 들어서 10 >> 2라고 한다면 10은 이진수로 1010₍₂₎이므로 2칸 밀면 10₍₂₎가 되는 것이다.
여기서 이해할 수 있는 것은, A << B를 한다면 A라는 이진수를 B칸씩 밀게 되는데, 그러면 모든 1의 값이 저장된 비트가 2^B씩 곱해지는 것이다.
그리고 A >> B는 A라는 이진수를 우측으로 B만큼 밀게 되니까 2^B만큼 나누어지게 된다. 따라서 다음과 같다.
A << B = A * 2^B
A >> B = A / 2^B
이를 통해 곱셈 / 나눗셈 산술 연산을 비트연산으로도 표현이 가능하다. 예) (A+B) / 2 = (A+B) >> 1
참고로, 비트 연산은 +, -보다 연산 우선 순위가 낮다. 헷갈리지 않게 코딩할 때는 () 연산자를 잘 써서 헷갈리지 않게 해주자.
비트 연산으로 집합을 나타내는 법)
비트마스크는 정수로 집합을 나타내는 것이 가능하다. 예를 들어 0~9 까지의 숫자로만 이루어지는 정수 집합이 있다고 할 때, 그 중 하나의 부분 집합이 A라고 하자. 그럼
A = {1, 3, 4, 5, 9} 라고 가정하면, 이를 570이라는 하나의 숫자로 나타낼 수 있다. 즉, A=570!
왜냐면, 아래와 같은 표를 보면 각각의 숫자가 있는 경우 1, 없는 경우 0으로 표시할 수 있기 때문이다.
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
그러면, 저 비트를 하나의 이진수라고 본다면 1000111010₍₂₎와 같으므로 10진수로 해보면 570이 되기 때문이다. 이 정수로 사용하게 되면 전체 저장 공간 또한 절약이 되고 정수이기 때문에 index로도 활용이 가능하므로 매우 큰 장점이 있다.
이 비트마스크로 집합을 나타낼 때는 0~N-1까지 정수로 이루어진 집합을 나타낼 때 사용된다. 1~N까지로 하면 1개의 비트가 더 필요하여 전체 공간이 2배가 된다.(시간도 2배가 됨) 그래서 0~N-1까지로 활용(또한, 0이 없으면 연산을 더 변형해야 함.)
그러면 아래에서 비트 연산을 어떻게 활용하는지 알아보자.
① 집합 포함 여부 검사
0~9까지의 숫자 중 해당 숫자가 현재 집합에 포함되어 있는지를 알아보는 방법이다.
{1, 3, 4, 5, 9} = 570이라고 할 때, 0이 포함된 여부를 검사하려면 0번째 비트만 1로 만들고 나머지를 0으로 한 것과 570을 2진수로 만든 것을 AND(&) 연산 하면 있는지를 알 수 있다.
왜냐하면, &연산은 둘 다 1인 경우만 1이므로 0이 포함된 경우는 1로 표시되기 때문에 그 결과로 나온 위치의 비트가 1이라면 해당 수가 집합에 포함 여부를 알 수 있기 때문이다.
아래의 그림을 보자.

위의 연산과 같이, 0이 포함되었는지 확인할 수 있는 비트만 1로 놓고 나머지를 0으로 둔 다음 확인을 하면 된다.
아래의 코드를 통해 사용 방법을 확인할 수 있다.
public class Main{
static int[] set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
static int sub_set = 570;
public static void main(String[] args){
// 현재 부분 집합에 0이 포함되었는지 검사
// 570 & 2^0 이므로 570 & (1 << 0) = 1이라면 있는 것, 0이면 없는 것
System.out.println((570 & (1 << 0)) == 1 ? "0 있음" : "0 없음" );
// 현재 부분 집합에 1이 포함되었는지 검사
// 570 & 2^1 이므로 570 & (1 << 1) = 2이라면 있는 것, 0이면 없는 것
System.out.println((570 & (1 << 1)) == 2 ? "1 있음" : "1 없음" );
// 현재 부분 집합에 2가 포함되었는지 검사
// 570 & 2^2 이므로 570 & (1 << 2) = 4이라면 있는 것, 0이면 없는 것
System.out.println((570 & (1 << 2)) == 4 ? "2 있음" : "2 없음" );
// 현재 부분 집합에 3이 포함되었는지 검사
// 570 & 2^3 이므로 570 & (1 << 3) = 8이라면 있는 것, 0이면 없는 것
System.out.println((570 & (1 << 3)) == 8 ? "3 있음" : "3 없음" );
System.out.println(check(4) ? "4 있음" : "4 없음" );
System.out.println(check(5) ? "5 있음" : "5 없음" );
System.out.println(check(6) ? "6 있음" : "6 없음" );
}
// 함수로 만든 경우
private static boolean check(int n){
boolean isExist = (sub_set & (1 << n)) == Math.pow(2, n) ? true : false;
return isExist;
}
}
/*
0 없음
1 있음
2 없음
3 있음
4 있음
5 있음
6 없음
*/
② 숫자 추가하기
위의 ①의 경우와 같이, 비트 연산을 통해 숫자를 추가할 수 있다. 특정 숫자를 추가하기 위해서는 해당 위치의 비트를 1로 만들어야 한다.
1도 만들기 위해서는 OR(|) 연산을 사용하면 된다. 추가하고자 하는 위치의 비트만 1로 만들고 나머지는 0으로 된 비트와 570을 2진수로 만든 비트를 OR 연산 시, 추가하고자 하는 비트 위치가 1로 변경되기 때문이다.
그림으로 알아보자. 만약 2를 추가하고자 한다면 아래와 같을 것이다.

코드로 알아보자.
public class Main{
static int[] set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
static int sub_set = 570;
public static void main(String[] args){
// 2를 추가
add(2);
System.out.println(sub_set);
// 7을 추가
add(7);
System.out.println(sub_set);
System.out.println(check(2) ? "2 있음" : "2 없음" );
System.out.println(check(7) ? "7 있음" : "7 없음" );
}
// 현재 특정 숫자를 추가하는 함수
private static void add(int n){
sub_set = sub_set | (1 << n);
}
// 현재 특정 숫자가 부분 집합에 있는지 체크하는 함수
private static boolean check(int n){
boolean isExist = (sub_set & (1 << n)) == Math.pow(2, n) ? true : false;
return isExist;
}
}
/*
결과
574
702
2 있음
7 있음
*/
③ 특정 숫자 제거하기
특정 숫자를 제거하기 위해서는 NOT(~) 연산과 AND(&) 연산을 같이 쓰면 된다.
NOT(~) 연산으로 제거하고자 하는 위치의 비트만 0으로 하고 나머지는 1로 만든 다음 AND(&) 연산을 하면 해당 위치만 0으로 바뀌고 나머지는 그대로가 되기 때문이다.
그림으로 알아보자. 4를 빼고자 한다면 다음과 같을 것이다.

코드로 알아보자.
public class Main{
static int[] set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
static int sub_set = 570;
public static void main(String[] args){
System.out.println(check(4) ? "4 있음" : "4 없음" );
// 4를 제거
delete(4);
System.out.println(check(4) ? "4 있음" : "4 없음" );
}
// 현재 특정 숫자를 제거하는 함수
private static void delete(int n){
sub_set = sub_set & ~(1 << n);
}
// 현재 특정 숫자가 부분 집합에 있는지 체크하는 함수
private static boolean check(int n){
boolean isExist = (sub_set & (1 << n)) == Math.pow(2, n) ? true : false;
return isExist;
}
}
/*
결과
4있음
4없음
*/
④ 토글 연산하기
0, 1을 왔다갔다 할 수 있게 하는 연산을 해보자. 만약 현재 있으면 없애고, 없으면 있게 하고자 한다면 어떨까?
즉, 0이면 1로 바꾸고, 1이면 0으로 바꾸고자 한다. 그러면 XOR(^) 연산을 수행하면 된다. XOR(^) 연산은 값이 다르면 1로 되며, 같으면 0이 되기 때문이다.
그림으로 알아보자. 3이라는 숫자를 토글하자면 다음과 같다.

코드로 구현한다면 다음과 같을 것이다.
public class Main{
static int[] set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
static int sub_set = 570;
public static void main(String[] args){
System.out.println(check(4) ? "4 있음" : "4 없음" );
// 4를 토글
toggle(4);
System.out.println(check(4) ? "4 있음" : "4 없음" );
}
// 현재 숫자 토글하기
private static void toggle(int n){
sub_set = sub_set ^ (1 << n);
}
// 현재 특정 숫자가 부분 집합에 있는지 체크하는 함수
private static boolean check(int n){
boolean isExist = (sub_set & (1 << n)) == Math.pow(2, n) ? true : false;
return isExist;
}
}
/*
결과
4있음
4없음
*/
⑤ 전체 집합, 공집합 표현하기
전체 집합은 모든 숫자가 1이라는 것이므로, N개의 비트가 모두 1이라는 의미이다. 따라서 전체 집합을 표시하는 방법은 다음과 같다.
0부터 시작하므로 좌측으로 N번 이동한 뒤 1을 빼면 된다.
전체 집합 : (1 << N) - 1
공집합은 그냥 0으로 표시하면 된다.
이제 위 방법을 응용하여 비트마스크를 이용한 완전 탐색 문제를 해결해볼 수 있다. 비트마스크는 보통 처리할 전체 데이터가 정해져 있고 그 안에서 특정 개수를 가지고 연산을 수행할 때 사용한다.
보통 재귀로도 풀 수 있는데 비트마스크를 이용해서도 해결이 가능하다.
⑤ BFS, DFS 사용하기
이는 그래프 자료 구조에서 모든 정점을 탐색하기 위한 방법이다.
BFS는 너비 우선 탐색으로 현재 정점과 인접한 정점을 우선으로 탐색하고 DFS는 깊이 우선 탐색으로 현재 인접한 정점을 탐색 후 그 다음 인접한 정점을 탐색하여 끝까지 탐색하는 방식이다.
이 내용은 그래프 관련 포스팅 BFS 포스팅, DFS 포스팅를 참고
⑥백트래킹이란?
이 글은 〈[되기] 코딩 테스트 합격자 되기(파이썬 편)〉에서 발췌했습니다.
깊이 우선 탐색, 너비 우선 탐색 방법은 데이터를 전부 확인하는 방법이다. 즉 완전 탐색이다. 완전 탐색은 모든 경우의 수를 탐색하는 방법이므로 대부분의 경우 비효율적이다.
예를 들어 출근하기 위해 아파트를 나섰는데 지하철 개찰구에 도착해서야 지갑을 두고 나온 사실을 알았다. 그러면 우선은 아파트로 돌아갈 것이다. 집으로 돌아가서 방을 하나씩 보면서 물건을 찾기 시작할 것 이다. 혹시라도 옆 집의 문 앞에 선 경우라도 금방 ‘아 옆 집이구나’하는 생각에 뒤로 돌아 우리 집으로 향할거다. 이렇게 어떤 가능성이 없는 곳을 알아보고 되돌아가는 것을 백트래킹(Backtracking)이라 한다.
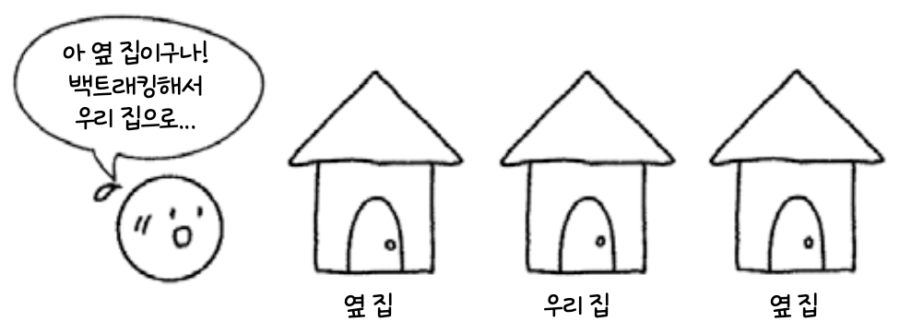
이렇게 가능성이 없는 곳에서는 되돌아가고, 가능성이 있는 곳을 탐색하는 알고리즘을 백트래킹 알고리즘이라고 한다.
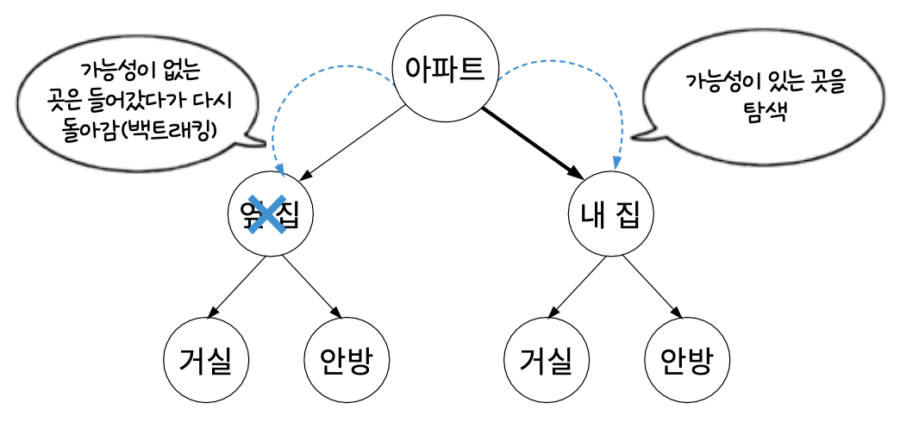
그림을 보면 답을 찾는 과정에서 가능성이 없는 곳에서는 백트래킹한다. 백트래킹 알고리즘은 문제마다 효율이 달라지므로 시간 복잡도를 특정하여 정의하기 어렵다. 하지만 확실한 것은 백트래킹을 통해 해가 될 가능성이 없는 탐색 대상을 배제할 수 있으므로 탐색 효율이 단순히 완전 탐색하는 방법보다 백트래킹이 효율적이다. 그럼 구체적인 예와 함께 백트래킹 알고리즘을 알자

유망 함수란?
백트래킹 알고리즘의 핵심은 ‘해가 될 가능성을 판단하는 것’이다. 그리고 그 가능성은 유망 함수라는 것을 정의하여 판단한다. 실제로 백트래킹 알고리즘은 다음과 같은 과정으로 진행한다.
- 유효한 해의 집합을 정의한다.
- 위 단계에서 정의한 집합을 그래프로 표현한다.
- 유망 함수를 정의한다.
- 백트래킹 알고리즘을 활용해서 해를 찾는다.
그렇다면 유망 함수가 백트래킹 알고리즘에서 어떻게 동작하는지 아주 간단한 문제를 풀어보며 알아보자.
합이 6을 넘는 경우 알아보기
{1, 2, 3, 4} 중 2개의 숫자를 뽑아서 합이 6을 초과하는 경우를 알아내는 백트래킹 알고리즘을 알아보자. 뽑는 순서가 다르면 다른 경우의 수로 간주한다. 예를 들어 {1, 3}과 {3, 1}의 합은 각각 4로 같지만 서로 다른 경우의 수다.
01단계 유효한 해의 집합을 정의한다. 서로 다른 두 수를 뽑는 경우의 수는 다음과 같다.

02단계 정의한 해의 집합을 그래프로 표현한다.
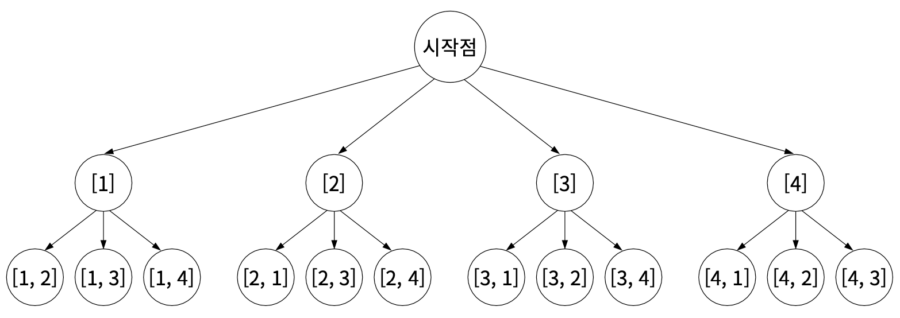
03단계 그래프에서 백트래킹을 수행한다. 여기서는 ‘처음에 뽑은 숫자가 3 미만이면 백트래킹한다’라는 전략을 사용한다. 다시 말해 1과 2를 처음에 뽑으면 이후에 어떤 경로로 가도 원하는 답이 나올 수 없으므로 1, 2는 아예 탐색을 시도하지도 않는다. 이렇게 특정 조건을 정의하는 것을 유망 함수(Promising Function)를 정의한다고 한다. 예를 들어 위 그림에서 1과 2는 유망 함수를 통과하지 못하여 백트래킹한다.
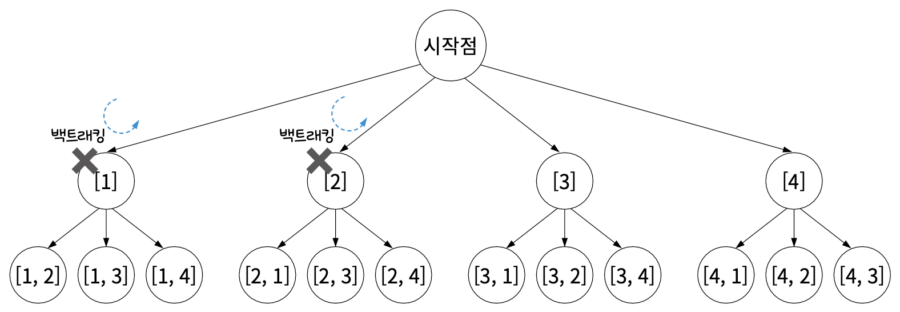
04단계 3은 유망 함수를 통과한다. 참고로 1, 2는 유망 함수와는 상관없이 깊이 우선 탐색 알고리즘에 의해 방문하지만 답이 아니므로 백트래킹하는 것이다. 그 이후 3 → 4로 가서야 답을 찾는다.
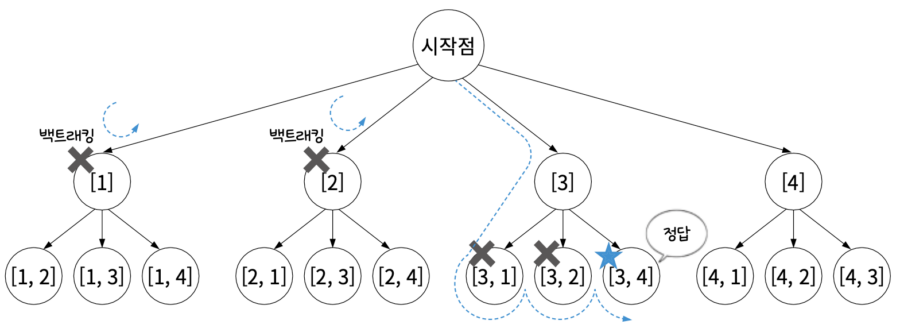
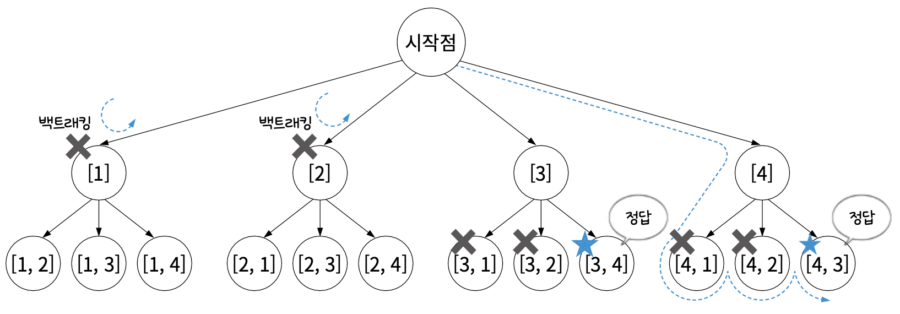
05단계 이와 같은 방식으로 나머지도 탐색을 진행하면된다.
완전 탐색의 시간 복잡도
| 알고리즘 | 시간 복잡도 |
| 브루트 포스 | O(nm) |
| 비트마스크 | O(2^n * n) |
| 백트래킹 | 최악의 경우, O(n!) |
| 순열 | O(n!) |
| 재귀함수 | O(n) |
| DFS/BFS | O(V+E) |
- 비트마스크 > DFS/BFS > Brute-Force > 재귀함수 > 순열 > 백트래킹
정리
| 알고리즘 종류 | 설명 | 장점 | 단점 |
| 브루트 포스 | ‘모든 경우의 수를 탐색’하면서 원하는 결과를 얻는 알고리즘을 의미합니다. | 가능한 모든 경우를 다 검사하기 때문에 예상된 결과를 얻을 수 있음 | 경우의 수가 많을 경우 시간이 오래 걸림 |
| 비트마스크 | ‘모든 경우의 수를 이진수로 표현‘하고 ‘비트 연산’을 통해 원하는 결과를 빠르게 얻는 알고리즘을 의미합니다. | 이진수 연산을 이용하여 계산 속도가 빠름 | 경우의 수가 많아질수록 메모리 사용량이 늘어남 |
| 백트래킹 | 결과를 얻기 위해 진행하는 도중에 ‘막히게 되면’ 그 지점으로 다시 돌아가서 ‘다른 경로를 탐색’하는 방식을 의미합니다. 결국 모든 가능한 경우의 수를 탐색하여 해결책을 찾습니다. | 경우의 수를 줄이면서도 모든 경우를 탐색할 수 있음 | 재귀 함수를 이용하기 때문에 스택 오버플로우가 발생할 가능성 있음 |
| 순열 | ‘순열을 이용하여 모든 경우의 수를 탐색‘하는 방법입니다. 순열은 서로 다른 n개 중에서 r개를 선택하여 나열하는 방법을 의미합니다 | 경우의 수가 적을 때 사용하면 유용함 | 경우의 수가 많을 경우 시간이 오래 걸림 |
| 재귀함수 | ‘자기 자신을 호출‘하여 모든 가능한 경우의 수를 체크하면서 최적의 해답을 얻는 방식을 의미합니다. | 코드가 간결하며, 이해하기 쉽습니다. | 스택 오버플로우가 발생할 가능성이 있음 |
| DFS/BFS | 깊이 우선 탐색(DFS: Depth-First Search) - 루트 노드에서 시작하여 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법을 의미합니다. 너비 우선 탐색(Breadth-First Search: BFS) - 루트 노드에서 시작하여 인접한 노드를 먼저 탐색하는 방법을 의미합니다. |
미로 찾기 등에 유용함 | 최악의 경우, 모든 노드를 다 방문해야 하므로 시간이 오래 걸림 |
참고자료
[1] 티스토리 : 겐지충 프로그래머 - 알고리즘 - 완전탐색(Exhaustive Search)
[2] 티스토리 : zo_zni`s Blog - 완전탐색 (Exhaustive search)
'🧠 Computer Science > Algorithm' 카테고리의 다른 글
| [정렬 알고리즘] 퀵 정렬(Quick Sort) (1) | 2025.02.19 |
|---|---|
| [정렬 알고리즘] 삽입 정렬(Insertion Sort) (0) | 2024.12.06 |
| [정렬 알고리즘] 선택 정렬(Selection Sort) (0) | 2024.11.30 |
| [정렬 알고리즘] 버블 정렬(Bubble Sort) (1) | 2024.11.29 |
| [그래프 탐색 알고리즘] DFS(깊이 우선 탐색) (0) | 2024.11.21 |

완전탐색❓
완전탐색은 알고리즘 패러다임중 하나로 가능한 모든 해를 찾아내어 그 중 조건을 만족하는 최적해를 찾아내는 방법이다. 완전탐색은 모든 가능성을 확인하기때문에 가장 정확하고 최적의 해를 구할 수 있지만, 시간복잡도가 매우 높아질 수 있다.
예를 들어, 4자리의 암호로 구성된 자물쇠를 풀려고 시도한다고 생각해보자. 이 자물쇠가 고장난 것이 아니라면, 반드시 해결할 수 있는 가장 확실한 방법은 0000 ~ 9999까지 모두 시도해보는 것이다.(최대 10,000번의 시도로 해결 가능)
모든 문제에 대해 완전탐색을 적용시키면 항상 답은 구해지겠지만 코딩테스트가 제한하는 시간안에 문제를 해결하지 못 할 가능성이 크다. 그렇기에 완전탐색을 사용해야 할 시점은 다음과 같다.
1. 주어진 입력의 범위가 작아 가능한 모든 해를 찾는 시간이 적게 들 때 즉, 시간 복잡도를 계산하고 될 거 같다 싶으면 일일이 다 하면 된다. 반복문이 몇 개든, 비효율적인 풀이 같아 보여도 상관없이 풀이를 작성해나가면 된다.
2. 코딩 테스트의 문제는 대체로 시간 복잡도가 10^8이내인 경우 통과가 된다. 그렇기에 입력의 범위가 100과 같이 작은 경우 완전 탐색으로 걸리는 시간 복잡도가 O(n^2)이라면 해당 방법은 10^4의 시간 복잡도를 갖기에 통과가 될 것이다. 이와 같이 주어진 입력의 범위가 작아 완전 탐색의 시간 복잡도 또한 낮아지는 경우 완전 탐색으로 빠르게 구현하여 문제를 해결할 수 있다.
3. 우선적으로 완전탐색으로 답을 구하고 그 과정을 최적화하여 시간을 줄이고 싶을 때
- 정렬
- 메모이제이션
- 투포인터
- DP
- 백트래킹
- 이진탐색
4. 주어진 입력의 범위가 커서 완전 탐색으로는 시간제한을 맞추지 못하는 문제에도 우선 완전 탐색을 적용시키는 방법을 고려할 수 있다. 완전 탐색은 앞서 설명했듯이 문제를 푸는 가장 기초적인 방법이다. 그렇기에 완전 탐색을 우선 구현한 후 해당 방법을 개선해 나감으로써 시간제한을 맞출 수 있다. 또한 완전 탐색을 통해 진행되는 문제의 과정을 보고 문제의 유형을 파악할 수 있는 등 문제의 명확한 풀이 방법을 찾지 못했을 경우에는 우선 완전 탐색으로 구현하는 것도 좋은 방법이다.
❔ 완전 탐색 vs 브루트 포스
위 완전 탐색과 브루트 포스는 종종 혼용되어 사용하는데 차이는 존재한다. 두 패러다임 모두 가능한 모든 해를 찾아내는 것은 같지만, 완전 탐색은 그 모든 해를 찾아나가는 과정이 보다 체계적인 방면 브루트 포스는 모든 해를 찾아나가는 과정이 이름 그대로 무식(Brute) 하게 모든 해를 찾아나간다는 것이 패러다임의 차이다. 하지만 많은 강의에서 두 용어를 엄밀하게 구분하진 않는다.
❔선형 탐색 vs 완전 탐색
1차원 배열에서 최댓값 찾기같은 문제는 배열을 처음부터 끝까지 한 번씩 확인하면서 현재 최댓값을 갱신해나가는 문제인데 그렇다면 각 요소를 반드시 다 확인하니 이 문제 또한 완전 탐색 알고리즘에 속하는것이 아닌지 궁금해졌다. 결론부터 말하면 완전 탐색 알고리즘이 아닌 선형(순차) 탐색 알고리즘이다.
🔹 선형 탐색 (Linear Search)
- 특정 데이터 구조(대부분 1차원 배열)에서 앞에서부터 하나씩 확인해서 원하는 값을 찾는 단순한 탐색 방법이다.
- 보통 O(n) 시간 복잡도
- 목적: 어떤 값이 존재하는지 여부만 확인
🔹 완전 탐색 (Brute-force Search)
- 어떤 문제를 풀기 위해 가능한 모든 조합/경우의 수를 시도해보는 전략.
- 예: 순열, 조합, 부분집합, 백트래킹, 비트마스크 등
- 보통 O(2ⁿ), O(n!) 같은 매우 큰 시간복잡도를 가짐.
- 목적: 조건을 만족하는 최적의 해 또는 모든 해를 찾기 위함.
🔹 차이점
| 항목 | 선형 탐색 | 완전 탐색 |
| 탐색 목적 | 원하는 값(조건을 만족하는 값)이 있는지만 확인 | 최적의 해 또는 모든 해를 찾기 위함 |
| 종료 조건 | 원하는 값 발견 시 즉시 탐색 종료 가능 | 모든 경우를 시도해야 하므로 끝까지 수행해야 함 |
| 탐색 범위 | 단일 데이터 구조(배열 등)에서의 순차적 확인 | 가능한 모든 조합, 순열, 경로 등을 전부 확인 |
| 시간 복잡도 | O(n) | O(n!), O(2ⁿ), O(n^r) 등 다양하고 큼 |
| 전략 성격 | 단순 탐색 | 문제 해결을 위한 포괄적 전략 |
완전탐색 기법을 활용하는 방법❗
우선 완전탐색 기법으로 문제를 풀기 위해서는 다음과 같이 고려해서 수행한다.
1) 해결하고자 하는 문제의 가능한 경우의 수를 대략적으로 계산한다.
2) 가능한 모든 방법을 다 고려한다.
3) 실제 답을 구할 수 있는지 적용한다.
여기서 2)의 모든 방법에는 다음과 같은 방법 등이 있다.
- Brute Force 기법 - 반복 / 조건문을 활용해 모두 테스트하는 방법
- 순열(Permutation), 조합(Combination)
- 재귀 호출
- 비트마스크 - 2진수 표현 기법을 활용하는 방법
- BFS, DFS를 활용하는 방법
- 백트래킹
각 방식에 대한 설명✔️
① Brute Force 기법
이 방법은 반복 / 조건문을 통해 가능한 모든 방법을 단순히 찾는 경우를 의미한다. 예를 들어, 위의 자물쇠 암호를 찾는 경우와 같이 모든 경우를 다 참조하는 경우가 그러하다.
② 순열(Permutation), 조합(Combination)
순열은 서로 다른 n개 중에서 순서를 생각하며 r개를 택하는 경우의 수를 의미한다.
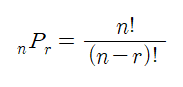
수식으로는 P(n, r) = n! / (n-r)!로 나타낼 수 있다. 전체 집합의 부분집합으로 볼 수 있는데 이로 인해 완전탐색 알고리즘 범주안에 있기도 하며, 시간복잡도는 O(n!)을 가진다.
// 순열 구현 코드
import java.util.Arrays;
public class Permutation {
static int count;
public static void main(String[] args) {
String[] stringArray = new String[]{"A", "B", "C"};
permutation(0, 2, 0, stringArray); // 두 번째 파라미터 값만 조정
System.out.println("총 갯수: " + count); // 총 갯수: 6
}
public static void permutation(int n, int r, int depth, String[] array) {
if(n >= array.length || depth >= r) {
System.out.println(Arrays.toString(Arrays.copyOf(array, r)));
count++;
return;
}
for(int a=n; a<array.length; a++) {
String temp = array[a];
array[a] = array[n];
array[n] = temp;
permutation(n+1, r, depth+1, array);
temp = array[a];
array[a] = array[n];
array[n] = temp;
}
}
}
순열 시간복잡도
컴퓨터에서 10의 8승은 굉장히 많은 것을 의미하고 있다. 언어에 따라 다를 수 있지만 기본적으로 컴퓨터의 10^8번 계산은 1초가 걸린다.
알고리즘 문제를 풀이할 때 입력 조건과 제한시간이 존재한다. 이때 입력 조건 n이 최대 범위가 100이라 하는 경우에 제한시간이 1초라면 대략 시간 복잡도 O(n^3) 풀이가 통과된다. (100*100*100=10^8)
다른 문제의 예시로 입력조건 n이 최대 범위가 10^8승이고 제한시간이 1초인 경우 시간 복잡도 O(n)의 풀이인 알고리즘을 선택해야 풀 수 있는 것이다.
입력 범위와 제한시간에 따라 선택 알고리즘이 달라진다는 것은 당연하게 받아들일 수 있지만,
10^8이 1초라는 사실에 입각하여 입력범위와 제한시간에 따라 가능한 시간복잡도를 알게 된다면 문제에 대한 알고리즘을 명확하게 선택할 수 있게 된다.
위에서 10^8이 무엇인지 알게 되었다면, 완전탐색 알고리즘이 가능한 문제를 알 수 있게 될 것이다. 완전탐색의 시간 복잡도의 경우 방법에 따라 다르기도 하지만 순열과 같이 오래 걸리는 경우는 O(2^n)과 O(n!)처럼 매우 오래 걸리는 경향이 있다.
하지만 1초는 10^8 임을 알고 있기 때문에 시간복잡도와 제한시간을 비교해 볼 수 있다. 입력조건의 최대범위를 시간복잡도 n에 대입하여 계산하여 제한시간과 비교할 수 있는 것이다.
이때 완전탐색의 시간복잡도가 제한시간 범위 안에 들어간다면, 완전탐색의 단점인 메모리와 시간이 오래 걸린다는 점은 무시한 채 쉬운 로직과 정확한 목푯값을 알 수 있는 장점을 활용할 수 있는 것이다.
순열의 경우의 수는 N!이므로 완전 탐색을 이용하기 위해서는 N이 한자리 수 정도는 되어야 한다.
N!은 굉장히 높은 시간 복잡도를 갖는다. N=10이면 되어도 약 360만 번의 연산이 수행되며 N=11이 되면 4억 번의 연산이 필요하다. 따라서 이 방법은 항상 사용할 수는 없고, 문제에서 주어진 N의 크기를 고려해야 한다.
✅ 순열이 완전 탐색인 이유
문제에서 “어떤 순서로 뭔가를 처리해야 하는 경우”, 예를 들어
- 여러 도시를 특정 순서로 방문할 때 (→ 여행 경로 문제)
- 숫자 카드를 순서대로 나열해서 조건에 맞는 경우를 찾을 때
- 특정 작업을 어떤 순서로 해야 할 때
이럴 때 모든 가능한 순서를 만들어보고, 그중에서 조건에 맞는 경우 즉, 정답을 찾는 방식은 완전 탐색이다.
예시①
[1, 2, 3]이라는 숫자가 있을 때, 이 세 숫자를 모두 사용해서 만들 수 있는 순열은
- [1, 2, 3]
- [1, 3, 2]
- [2, 1, 3]
- [2, 3, 1]
- [3, 1, 2]
- [3, 2, 1]
총 3! = 6가지 경우가 있다.
이건 세 수의 모든 순서를 다 만들어본 것, 즉 모든 경우의 수를 탐색한 것이니까 완전 탐색이다.
예시②
[1, 2, 3]이라는 숫자가 있을 때, 세 숫자 중 2개를 선택하여 숫자를 모든 순서대로 뽑는 경우의 순열은
- [1, 2]
- [1, 3]
- [2, 1]
- [2, 3]
- [3, 1]
- [3, 2]
순열 예제 - 가장 큰 두 자리 수 구하기
import java.util.*;
public class Permutation {
static int N = 4;
static int[] Nums = {1, 2, 3, 4};
static int solve(int cnt, int used, int val) {
if(cnt == 2) return val;
int ret = 0;
for(int i=0; i<N; ++i) {
if((used & 1 << i) != 0) continue;
ret = Math.max(ret, solve(cnt + 1, used | 1 << i, val * 10 +Nums[i]));
}
return ret;
}
public static void main(String[] args) {
System.out.println(solve(0, 0, 0));
}
}
// 출력:43
// 출처 : https://www.youtube.com/watch?v=CDLBg6wbhUQ
// 순열의 다른 구현 방법들 : https://define-me.tistory.com/178
조합이란 서로 다른 n개중에서 순서 상관 없이 r개를 선택하는 경우의 수를 의미한다. (순서 상관 없음)
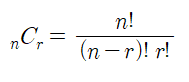
// 조합 구현 코드
public class Combination {
// 1. 백트래킹 구현
// 사용 예시 : combination(int[] arr, visited, 0, n, r)
static void combination(int[] arr, boolean[] visited, int start, int n, int r) {
if(r == 0) {
print(arr, visited, n);
return;
}
for(int i = start; i < n; i++) {
visited[i] = true;
combination(arr, visited, i + 1, n, r - 1);
visited[i] = false;
}
}
// 2. 재귀 사용
// 사용 예시 : comb(arr, visited, 0, n, r)
static void comb(int[] arr, boolean[] visited, int depth, int n, int r) {
if(r == 0) {
print(arr, visited, n);
return;
}
if(depth == n) {
return;
}
visited[depth] = true;
comb(arr, visited, depth + 1, n, r-1);
visited[depth] = false; // 빼먹지 않기!
comb(arr, visited, depth + 1, n, r);
}
public static void main(String[] args) {
int n = 4;
int[] arr = {1, 2, 3, 4};
boolean[] visited = new boolean[n];
for(int i = 1; i <= n; i++) {
System.out.println("\n" + n + "개 중에서" + i + "개 뽑기");
comb(arr, visited, 0, n, i);
}
for(int i = 1; i <= n; i++) {
System.out.println("\n" + n + "개 중에서" + i + "개 뽑기");
combination(arr, visited, 0, n, i);
}
}
// 배열 출력
static void print(int[] arr, boolean[] visited, int n) {
for (int i = 0; i < n; i++) {
if(visited[i]) {
System.out.print(arr[i] + " ");
}
}
System.out.println();
}
}
조합 예제 - 가장 큰 두 수의 합 구하기
import java.util.*;
public class Combination {
static int N = 4;
static int[] Nums = {1 ,2 ,3, 4};
static int solve(int pos, int cnt, int val) {
if(cnt == 2) return val;
if(pos == N) return -1;
int ret = 0;
ret = Math.max(ret, solve(pos + 1, cnt + 1, val + Nums[pos]));
ret = Math.max(ret, solve(pos +1, cnt, val));
return ret;
}
public static void main(String[] args) {
System.out.println(solve(0, 0, 0));
}
}
// 출력:7
// 출처 : https://www.youtube.com/watch?v=CDLBg6wbhUQ&t=40s
순열 조합 코딩테스트 문제
프로그래머스 순열 문제 - 피로도
백준 조합 문제 - 조합론
③ 재귀(Recursive)
재귀는 말 그대로 자기 자신을 호출한다는 의미이다. 왜 자기 자신을 호출할 필요가 있을까?
예를 들어, 총 4개의 숫자 중에 2개를 선택하는 경우를 모두 출력한다고 가정해보자. 1~4까지 숫자가 있고 2개를 중복 없이 선택하는 모든 경우의 수를 출력하고자 한다고 가정하자.
이를 반복문으로 표현한다면 다음과 같을 것이다.
public class Main {
public static void main(String[] args) {
for (int i = 1; i <= 4; i++) {
for (int j = i + 1; j <= 4; j++) {
System.out.println(i + " " + j);
}
}
}
}
// 출력
// 1 2
// 1 3
// 1 4
// 2 3
// 2 4
// 3 4손 쉽게 2중 반복문으로 해결하였다. 그런데.. 만약 숫자 N개의 숫자 중 M개를 고르는 경우라고 할 때, N과 M이 매우 큰 숫자라면 어떨까? 반복문을 수백, 수천 개를 써 내려갈 수는 없다!
이를 재귀 함수를 활용한다면 자기 자신을 호출함으로써 다음 숫자를 선택할 수 있도록 이동시켜 전체 코드를 매우 짧게 줄일 수 있다!
아래와 같이, 1~100의 숫자 중, 5개를 선택하는 경우를 코드로 작성해보자.
public class Main{
static int lim = 100; // 1~100까지의 제한
static int n = 5; // 5개만 고른다.
// chosen은 선택된 숫자가 저장된 배열
// curr은 현재 숫자를 선택하는 index
// cnt는 몇 개의 숫자가 선택되었는지 확인
private static void solve(int[] chosen, int curr, int cnt){
// n개의 숫자를 다 선택했다면 출력 후 더 이상 재귀를 돌지 않아야 한다!
// 탈출 조건의 정의!
if(cnt == n){
for(int i : chosen){
System.out.print(i + " ");
}
System.out.println();
return;
}
// 반복문을 통해 숫자를 계속 선택!
for(int i=curr+1; i <= lim; i++){
// 현재 선택된 숫자를 저장
chosen[cnt] = i;
// 다음 숫자를 선택하기 위해 재귀 호출
solve(chosen, curr, cnt+1);
}
}
public static void main(String[] args){
int[] chosen = new int[n]; // 선택된 숫자가 저장되는 배열
// 시작은 0부터 시작하며 0개를 현재 선택했으니 아래와 같이 parameter 전달!
solve(chosen, 0, 0);
}
}여기서 중요한 점!
⑴ 재귀를 탈출하기 위한 탈출 조건이 필요!
▶ 이것이 없으면 n개를 모두 골랐음에도 더 숫자를 선택하고자 하여 선택된 숫자를 저장하는 배열에 범위 초과 오류가 나거나, 다른 자료구조를 쓴 경우 잘못된 출력이 나올 수 있고, 혹은 무한 루프가 발생할 수 있다!
⑵ 현재 함수의 상태를 저장하는 Parameter가 필요!
▶ 위에서 우리는 curr, cnt를 통해 어떤 숫자까지 선택했는지, 몇 개를 선택했는지 전달하였다. 이것이 없다면 현재 함수의 상태를 저장할 수 없어 재귀 탈출 조건을 만들 수 없게 되거나 잘못된 결과를 출력하게 된다!
⑶ Return문을 신경 쓸 것!
▶ 위의 함수는 단순 출력이기에 void로 함수를 작성했다. 그런데, 재귀를 통해 이후의 연산 결과를 반환 후 이전 결과에 추가 연산을 수행하는 경우도 있을 수 있다. 즉, 문제 해결을 위한 정확한 정의를 수행하여야 이것을 완벽히 풀 수 있다.
잘 생각해보면 Dynamic Programming과도 매우 흡사해 보인다. 그 또한 Top-Down을 사용 시 재귀를 통해 수행하는데, 기저 사례를 통해 탈출 조건을 만들고, 현재 함수의 상태를 전달하는 Parameter를 전달한다.
또한 Return을 통해 필요한 값을 반환하여 정답을 구하는 연산 시에 사용하게 된다.
완전 탐색의 재귀와 DP의 차이점은, DP는 작은 문제가 큰 문제와 동일한 구조를 가져 큰 문제의 답을 구할 시에 작은 문제의 결과를 기억한 뒤 그대로 사용하여 수행 속도를 빠르게 한다는 것이다.
그에 반해 완전 탐색은 크고 작은 문제의 구조가 다를 수 있고, 이전 결과를 반드시 기억하는 것이 아니라 해결 가능한 방법을 모두 탐색한다는 차이가 있다.
(즉, DP는 일반적인 재귀 중 조건을 만족하는 경우에 적용 가능!)
④ 비트마스크(Bitmask)
비트마스크란 비트(bit) 연산을 통해서 부분 집합을 표현하는 방법을 의미한다.
비트 연산이란 다음과 같은 것들이 있다.
- AND 연산(&) : 둘 다 1이면 1
- OR 연산(|) : 둘 중 1개만 1이면 1
- NOT 연산(~) : 1이면 0, 0이면 1
- XOR 연산(^) : 둘의 관계가 다르면 1, 같으면 0
- Shift 연산(<<, >>) : A << B라고 한다면 A를 좌측으로 B 비트만큼 미는 것이다.
좀 더 쉽게 표로 알아보자. A, B라는 변수값이 있다고 할 때, 각각의 비트 연산결과를 표로 정리하였다.(Shift 연산은 아래에 별도로 정리함)
| A | B | A&B | A|B | ~A | A^B |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
그런데 우리는 1, 0만을 사용할 것이 아니라 각 모든 숫자를 비트 연산할 수 있어야 한다. 모든 숫자는 2진수로 표현될 수 있기 때문에 2진수를 통해 비트연산을 수행할 수 있다.
만약, 13과 72를 2진수로 나타낸다면 어떨까? 다음과 같을 것이다.
13 = 1101₍₂₎
72 = 1001000₍₂₎
그러면 13의 경우에는 부족한 앞의 3자리를 0으로 채우고 비트연산을 수행할 수 있다. 그 결과는 다음과 같다.

비트 연산의 시간복잡도는 내부적으로 상수 시간 정도로 처리가 되어 O(1)이라고 보면 된다.(그렇다고 프로그래밍 시 산술 연산을 비트 연산으로 모두 바꾸는 것은 오히려 비효율적. 유지보수에도 좋지 않고 실제로 미미한 차이만 나기 때문이다..)
NOT (^)연산 사용 시 주의할 점
코딩 시, 숫자들을 저장할 수 있는 자료형은 1가지가 아니다. Java의 경우 byte, short, int, long 형으로 정수 형태의 자료를 저장할 수 있다.
이 때, byte는 8비트, short는 16비트, int는 32비트, long은 64비트이기 때문에 전체 저장할 수 있는 비트의 수가 다르므로 어떤 자료형에서 NOT연산을 하느냐에 따라 숫자 자체의 결과는 같더라도 비트마스크 결과는 다를 수 있다.
예를 들어 40을 byte, short, int 형으로 저장한 뒤 각각을 NOT연산도 수행해보고, 비트 출력 또한 수행해보자.
public class Main{
public static void main(String[] args){
byte b = 40;
short s = 40;
int i = 40;
// byte, short는 toBinaryString이 없어 Integer클래스의 함수를 빌려와서 연산한다.
// 0xFF는 8비트로 11111111이므로 & 연산을 통해 결과를 나타낼 수 있다.
String bs = String.format("%8s", Integer.toBinaryString(~b & 0xFF));
System.out.println("Byte 형 40 NOT 연산 : " + ~b + ", 2진수 출력 : " + bs);
// 0xFFFF는 16비트로 1111111111111111이므로 & 연산을 통해 결과를 나타낼 수 있다.
String ss = String.format("%16s", Integer.toBinaryString(~s & 0xFFFF)).replace(' ', '0');
System.out.println("Short 형 40 NOT 연산 : " + ~s + ", 2진수 출력 : " + ss);
System.out.println("Integer 형 40 NOT 연산 : " + ~i + ", 2진수 출력 : " + Integer.toBinaryString(~i));
}
}
/* 결과
Byte 형 40 NOT 연산 : -41, 2진수 출력 : 11010111
Short 형 40 NOT 연산 : -41, 2진수 출력 : 1111111111010111
Integer 형 40 NOT 연산 : -41, 2진수 출력 : 11111111111111111111111111010111
*/위와 같이 숫자 자체는 같더라도 전체 비트 결과는 다르므로 주의해서 사용해야 한다. 만약 C++를 사용한다면 signed, unsigned 형까지 고려해서 연산을 수행해야 한다.
Shift 연산
그럼 Shift 연산에 대해서도 알아보자. <<, >> 로 표현하며 해당 방향으로 원 비트를 특정 값만큼 밀어버린다는 개념으로 이해하면 된다.
예를 들어서 1 << 3 이라고 한다면 어떨까? 1은 이진수로 1₍₂₎인데, 이를 3칸 좌측으로 밀어버리므로 1000₍₂₎가 된다.
그렇다면 7 << 3이라고 한다면 7000이 되나? 아니다. 7을 2진수로 변환한다음 3칸 밀어야 한다. 즉, 7은 이진수로 111₍₂₎ 이므로 3칸 좌측으로 밀면 111000₍₂₎가 된다.
반대로 >>는 우측으로 밀어버리는 것인데, 우측으로 밀어버리면 버려지는 것들은 어떻게 할까? 그냥 삭제되는 것이다. 예를 들어서 10 >> 2라고 한다면 10은 이진수로 1010₍₂₎이므로 2칸 밀면 10₍₂₎가 되는 것이다.
여기서 이해할 수 있는 것은, A << B를 한다면 A라는 이진수를 B칸씩 밀게 되는데, 그러면 모든 1의 값이 저장된 비트가 2^B씩 곱해지는 것이다.
그리고 A >> B는 A라는 이진수를 우측으로 B만큼 밀게 되니까 2^B만큼 나누어지게 된다. 따라서 다음과 같다.
A << B = A * 2^B
A >> B = A / 2^B
이를 통해 곱셈 / 나눗셈 산술 연산을 비트연산으로도 표현이 가능하다. 예) (A+B) / 2 = (A+B) >> 1
참고로, 비트 연산은 +, -보다 연산 우선 순위가 낮다. 헷갈리지 않게 코딩할 때는 () 연산자를 잘 써서 헷갈리지 않게 해주자.
비트 연산으로 집합을 나타내는 법)
비트마스크는 정수로 집합을 나타내는 것이 가능하다. 예를 들어 0~9 까지의 숫자로만 이루어지는 정수 집합이 있다고 할 때, 그 중 하나의 부분 집합이 A라고 하자. 그럼
A = {1, 3, 4, 5, 9} 라고 가정하면, 이를 570이라는 하나의 숫자로 나타낼 수 있다. 즉, A=570!
왜냐면, 아래와 같은 표를 보면 각각의 숫자가 있는 경우 1, 없는 경우 0으로 표시할 수 있기 때문이다.
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
그러면, 저 비트를 하나의 이진수라고 본다면 1000111010₍₂₎와 같으므로 10진수로 해보면 570이 되기 때문이다. 이 정수로 사용하게 되면 전체 저장 공간 또한 절약이 되고 정수이기 때문에 index로도 활용이 가능하므로 매우 큰 장점이 있다.
이 비트마스크로 집합을 나타낼 때는 0~N-1까지 정수로 이루어진 집합을 나타낼 때 사용된다. 1~N까지로 하면 1개의 비트가 더 필요하여 전체 공간이 2배가 된다.(시간도 2배가 됨) 그래서 0~N-1까지로 활용(또한, 0이 없으면 연산을 더 변형해야 함.)
그러면 아래에서 비트 연산을 어떻게 활용하는지 알아보자.
① 집합 포함 여부 검사
0~9까지의 숫자 중 해당 숫자가 현재 집합에 포함되어 있는지를 알아보는 방법이다.
{1, 3, 4, 5, 9} = 570이라고 할 때, 0이 포함된 여부를 검사하려면 0번째 비트만 1로 만들고 나머지를 0으로 한 것과 570을 2진수로 만든 것을 AND(&) 연산 하면 있는지를 알 수 있다.
왜냐하면, &연산은 둘 다 1인 경우만 1이므로 0이 포함된 경우는 1로 표시되기 때문에 그 결과로 나온 위치의 비트가 1이라면 해당 수가 집합에 포함 여부를 알 수 있기 때문이다.
아래의 그림을 보자.

위의 연산과 같이, 0이 포함되었는지 확인할 수 있는 비트만 1로 놓고 나머지를 0으로 둔 다음 확인을 하면 된다.
아래의 코드를 통해 사용 방법을 확인할 수 있다.
public class Main{
static int[] set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
static int sub_set = 570;
public static void main(String[] args){
// 현재 부분 집합에 0이 포함되었는지 검사
// 570 & 2^0 이므로 570 & (1 << 0) = 1이라면 있는 것, 0이면 없는 것
System.out.println((570 & (1 << 0)) == 1 ? "0 있음" : "0 없음" );
// 현재 부분 집합에 1이 포함되었는지 검사
// 570 & 2^1 이므로 570 & (1 << 1) = 2이라면 있는 것, 0이면 없는 것
System.out.println((570 & (1 << 1)) == 2 ? "1 있음" : "1 없음" );
// 현재 부분 집합에 2가 포함되었는지 검사
// 570 & 2^2 이므로 570 & (1 << 2) = 4이라면 있는 것, 0이면 없는 것
System.out.println((570 & (1 << 2)) == 4 ? "2 있음" : "2 없음" );
// 현재 부분 집합에 3이 포함되었는지 검사
// 570 & 2^3 이므로 570 & (1 << 3) = 8이라면 있는 것, 0이면 없는 것
System.out.println((570 & (1 << 3)) == 8 ? "3 있음" : "3 없음" );
System.out.println(check(4) ? "4 있음" : "4 없음" );
System.out.println(check(5) ? "5 있음" : "5 없음" );
System.out.println(check(6) ? "6 있음" : "6 없음" );
}
// 함수로 만든 경우
private static boolean check(int n){
boolean isExist = (sub_set & (1 << n)) == Math.pow(2, n) ? true : false;
return isExist;
}
}
/*
0 없음
1 있음
2 없음
3 있음
4 있음
5 있음
6 없음
*/
② 숫자 추가하기
위의 ①의 경우와 같이, 비트 연산을 통해 숫자를 추가할 수 있다. 특정 숫자를 추가하기 위해서는 해당 위치의 비트를 1로 만들어야 한다.
1도 만들기 위해서는 OR(|) 연산을 사용하면 된다. 추가하고자 하는 위치의 비트만 1로 만들고 나머지는 0으로 된 비트와 570을 2진수로 만든 비트를 OR 연산 시, 추가하고자 하는 비트 위치가 1로 변경되기 때문이다.
그림으로 알아보자. 만약 2를 추가하고자 한다면 아래와 같을 것이다.

코드로 알아보자.
public class Main{
static int[] set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
static int sub_set = 570;
public static void main(String[] args){
// 2를 추가
add(2);
System.out.println(sub_set);
// 7을 추가
add(7);
System.out.println(sub_set);
System.out.println(check(2) ? "2 있음" : "2 없음" );
System.out.println(check(7) ? "7 있음" : "7 없음" );
}
// 현재 특정 숫자를 추가하는 함수
private static void add(int n){
sub_set = sub_set | (1 << n);
}
// 현재 특정 숫자가 부분 집합에 있는지 체크하는 함수
private static boolean check(int n){
boolean isExist = (sub_set & (1 << n)) == Math.pow(2, n) ? true : false;
return isExist;
}
}
/*
결과
574
702
2 있음
7 있음
*/
③ 특정 숫자 제거하기
특정 숫자를 제거하기 위해서는 NOT(~) 연산과 AND(&) 연산을 같이 쓰면 된다.
NOT(~) 연산으로 제거하고자 하는 위치의 비트만 0으로 하고 나머지는 1로 만든 다음 AND(&) 연산을 하면 해당 위치만 0으로 바뀌고 나머지는 그대로가 되기 때문이다.
그림으로 알아보자. 4를 빼고자 한다면 다음과 같을 것이다.

코드로 알아보자.
public class Main{
static int[] set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
static int sub_set = 570;
public static void main(String[] args){
System.out.println(check(4) ? "4 있음" : "4 없음" );
// 4를 제거
delete(4);
System.out.println(check(4) ? "4 있음" : "4 없음" );
}
// 현재 특정 숫자를 제거하는 함수
private static void delete(int n){
sub_set = sub_set & ~(1 << n);
}
// 현재 특정 숫자가 부분 집합에 있는지 체크하는 함수
private static boolean check(int n){
boolean isExist = (sub_set & (1 << n)) == Math.pow(2, n) ? true : false;
return isExist;
}
}
/*
결과
4있음
4없음
*/
④ 토글 연산하기
0, 1을 왔다갔다 할 수 있게 하는 연산을 해보자. 만약 현재 있으면 없애고, 없으면 있게 하고자 한다면 어떨까?
즉, 0이면 1로 바꾸고, 1이면 0으로 바꾸고자 한다. 그러면 XOR(^) 연산을 수행하면 된다. XOR(^) 연산은 값이 다르면 1로 되며, 같으면 0이 되기 때문이다.
그림으로 알아보자. 3이라는 숫자를 토글하자면 다음과 같다.

코드로 구현한다면 다음과 같을 것이다.
public class Main{
static int[] set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
static int sub_set = 570;
public static void main(String[] args){
System.out.println(check(4) ? "4 있음" : "4 없음" );
// 4를 토글
toggle(4);
System.out.println(check(4) ? "4 있음" : "4 없음" );
}
// 현재 숫자 토글하기
private static void toggle(int n){
sub_set = sub_set ^ (1 << n);
}
// 현재 특정 숫자가 부분 집합에 있는지 체크하는 함수
private static boolean check(int n){
boolean isExist = (sub_set & (1 << n)) == Math.pow(2, n) ? true : false;
return isExist;
}
}
/*
결과
4있음
4없음
*/
⑤ 전체 집합, 공집합 표현하기
전체 집합은 모든 숫자가 1이라는 것이므로, N개의 비트가 모두 1이라는 의미이다. 따라서 전체 집합을 표시하는 방법은 다음과 같다.
0부터 시작하므로 좌측으로 N번 이동한 뒤 1을 빼면 된다.
전체 집합 : (1 << N) - 1
공집합은 그냥 0으로 표시하면 된다.
이제 위 방법을 응용하여 비트마스크를 이용한 완전 탐색 문제를 해결해볼 수 있다. 비트마스크는 보통 처리할 전체 데이터가 정해져 있고 그 안에서 특정 개수를 가지고 연산을 수행할 때 사용한다.
보통 재귀로도 풀 수 있는데 비트마스크를 이용해서도 해결이 가능하다.
⑤ BFS, DFS 사용하기
이는 그래프 자료 구조에서 모든 정점을 탐색하기 위한 방법이다.
BFS는 너비 우선 탐색으로 현재 정점과 인접한 정점을 우선으로 탐색하고 DFS는 깊이 우선 탐색으로 현재 인접한 정점을 탐색 후 그 다음 인접한 정점을 탐색하여 끝까지 탐색하는 방식이다.
이 내용은 그래프 관련 포스팅 BFS 포스팅, DFS 포스팅를 참고
⑥백트래킹이란?
이 글은 〈[되기] 코딩 테스트 합격자 되기(파이썬 편)〉에서 발췌했습니다.
깊이 우선 탐색, 너비 우선 탐색 방법은 데이터를 전부 확인하는 방법이다. 즉 완전 탐색이다. 완전 탐색은 모든 경우의 수를 탐색하는 방법이므로 대부분의 경우 비효율적이다.
예를 들어 출근하기 위해 아파트를 나섰는데 지하철 개찰구에 도착해서야 지갑을 두고 나온 사실을 알았다. 그러면 우선은 아파트로 돌아갈 것이다. 집으로 돌아가서 방을 하나씩 보면서 물건을 찾기 시작할 것 이다. 혹시라도 옆 집의 문 앞에 선 경우라도 금방 ‘아 옆 집이구나’하는 생각에 뒤로 돌아 우리 집으로 향할거다. 이렇게 어떤 가능성이 없는 곳을 알아보고 되돌아가는 것을 백트래킹(Backtracking)이라 한다.

이렇게 가능성이 없는 곳에서는 되돌아가고, 가능성이 있는 곳을 탐색하는 알고리즘을 백트래킹 알고리즘이라고 한다.

그림을 보면 답을 찾는 과정에서 가능성이 없는 곳에서는 백트래킹한다. 백트래킹 알고리즘은 문제마다 효율이 달라지므로 시간 복잡도를 특정하여 정의하기 어렵다. 하지만 확실한 것은 백트래킹을 통해 해가 될 가능성이 없는 탐색 대상을 배제할 수 있으므로 탐색 효율이 단순히 완전 탐색하는 방법보다 백트래킹이 효율적이다. 그럼 구체적인 예와 함께 백트래킹 알고리즘을 알자

유망 함수란?
백트래킹 알고리즘의 핵심은 ‘해가 될 가능성을 판단하는 것’이다. 그리고 그 가능성은 유망 함수라는 것을 정의하여 판단한다. 실제로 백트래킹 알고리즘은 다음과 같은 과정으로 진행한다.
- 유효한 해의 집합을 정의한다.
- 위 단계에서 정의한 집합을 그래프로 표현한다.
- 유망 함수를 정의한다.
- 백트래킹 알고리즘을 활용해서 해를 찾는다.
그렇다면 유망 함수가 백트래킹 알고리즘에서 어떻게 동작하는지 아주 간단한 문제를 풀어보며 알아보자.
합이 6을 넘는 경우 알아보기
{1, 2, 3, 4} 중 2개의 숫자를 뽑아서 합이 6을 초과하는 경우를 알아내는 백트래킹 알고리즘을 알아보자. 뽑는 순서가 다르면 다른 경우의 수로 간주한다. 예를 들어 {1, 3}과 {3, 1}의 합은 각각 4로 같지만 서로 다른 경우의 수다.
01단계 유효한 해의 집합을 정의한다. 서로 다른 두 수를 뽑는 경우의 수는 다음과 같다.

02단계 정의한 해의 집합을 그래프로 표현한다.

03단계 그래프에서 백트래킹을 수행한다. 여기서는 ‘처음에 뽑은 숫자가 3 미만이면 백트래킹한다’라는 전략을 사용한다. 다시 말해 1과 2를 처음에 뽑으면 이후에 어떤 경로로 가도 원하는 답이 나올 수 없으므로 1, 2는 아예 탐색을 시도하지도 않는다. 이렇게 특정 조건을 정의하는 것을 유망 함수(Promising Function)를 정의한다고 한다. 예를 들어 위 그림에서 1과 2는 유망 함수를 통과하지 못하여 백트래킹한다.

04단계 3은 유망 함수를 통과한다. 참고로 1, 2는 유망 함수와는 상관없이 깊이 우선 탐색 알고리즘에 의해 방문하지만 답이 아니므로 백트래킹하는 것이다. 그 이후 3 → 4로 가서야 답을 찾는다.

05단계 이와 같은 방식으로 나머지도 탐색을 진행하면된다.

완전 탐색의 시간 복잡도
| 알고리즘 | 시간 복잡도 |
| 브루트 포스 | O(nm) |
| 비트마스크 | O(2^n * n) |
| 백트래킹 | 최악의 경우, O(n!) |
| 순열 | O(n!) |
| 재귀함수 | O(n) |
| DFS/BFS | O(V+E) |
- 비트마스크 > DFS/BFS > Brute-Force > 재귀함수 > 순열 > 백트래킹
정리
| 알고리즘 종류 | 설명 | 장점 | 단점 |
| 브루트 포스 | ‘모든 경우의 수를 탐색’하면서 원하는 결과를 얻는 알고리즘을 의미합니다. | 가능한 모든 경우를 다 검사하기 때문에 예상된 결과를 얻을 수 있음 | 경우의 수가 많을 경우 시간이 오래 걸림 |
| 비트마스크 | ‘모든 경우의 수를 이진수로 표현‘하고 ‘비트 연산’을 통해 원하는 결과를 빠르게 얻는 알고리즘을 의미합니다. | 이진수 연산을 이용하여 계산 속도가 빠름 | 경우의 수가 많아질수록 메모리 사용량이 늘어남 |
| 백트래킹 | 결과를 얻기 위해 진행하는 도중에 ‘막히게 되면’ 그 지점으로 다시 돌아가서 ‘다른 경로를 탐색’하는 방식을 의미합니다. 결국 모든 가능한 경우의 수를 탐색하여 해결책을 찾습니다. | 경우의 수를 줄이면서도 모든 경우를 탐색할 수 있음 | 재귀 함수를 이용하기 때문에 스택 오버플로우가 발생할 가능성 있음 |
| 순열 | ‘순열을 이용하여 모든 경우의 수를 탐색‘하는 방법입니다. 순열은 서로 다른 n개 중에서 r개를 선택하여 나열하는 방법을 의미합니다 | 경우의 수가 적을 때 사용하면 유용함 | 경우의 수가 많을 경우 시간이 오래 걸림 |
| 재귀함수 | ‘자기 자신을 호출‘하여 모든 가능한 경우의 수를 체크하면서 최적의 해답을 얻는 방식을 의미합니다. | 코드가 간결하며, 이해하기 쉽습니다. | 스택 오버플로우가 발생할 가능성이 있음 |
| DFS/BFS | 깊이 우선 탐색(DFS: Depth-First Search) - 루트 노드에서 시작하여 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법을 의미합니다. 너비 우선 탐색(Breadth-First Search: BFS) - 루트 노드에서 시작하여 인접한 노드를 먼저 탐색하는 방법을 의미합니다. |
미로 찾기 등에 유용함 | 최악의 경우, 모든 노드를 다 방문해야 하므로 시간이 오래 걸림 |
참고자료
[1] 티스토리 : 겐지충 프로그래머 - 알고리즘 - 완전탐색(Exhaustive Search)
[2] 티스토리 : zo_zni`s Blog - 완전탐색 (Exhaustive search)
'🧠 Computer Science > Algorithm' 카테고리의 다른 글
| [정렬 알고리즘] 퀵 정렬(Quick Sort) (1) | 2025.02.19 |
|---|---|
| [정렬 알고리즘] 삽입 정렬(Insertion Sort) (0) | 2024.12.06 |
| [정렬 알고리즘] 선택 정렬(Selection Sort) (0) | 2024.11.30 |
| [정렬 알고리즘] 버블 정렬(Bubble Sort) (1) | 2024.11.29 |
| [그래프 탐색 알고리즘] DFS(깊이 우선 탐색) (0) | 2024.11.21 |
