선형대수학이란?
선형대수학은 벡터 공간, 벡터, 선형 변환, 행렬, 연립 선형 방정식 등을 연구하는 대수학의 한 분야이다. 특히 AI 분야에서는 데이터의 특징을 추출하고 분석하기 위해 행렬과 벡터를 활용하며, 신경망의 가중치 조정과 같은 연산에서 선형 대수학의 원리를 적용하여 활용되고 있으며 선형대수학의 중요성은 점점 더 커지고 있다.
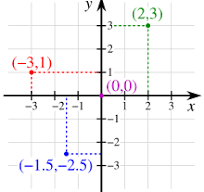
2차원 좌표계에서의 일차방정식
2차원 좌표계에서 직선은 다음과 같은 형태로 표현할 수 있다.
ax + by = c (단, a ≠ 0, b ≠ 0)
3차원 좌표계에서의 일차방정식
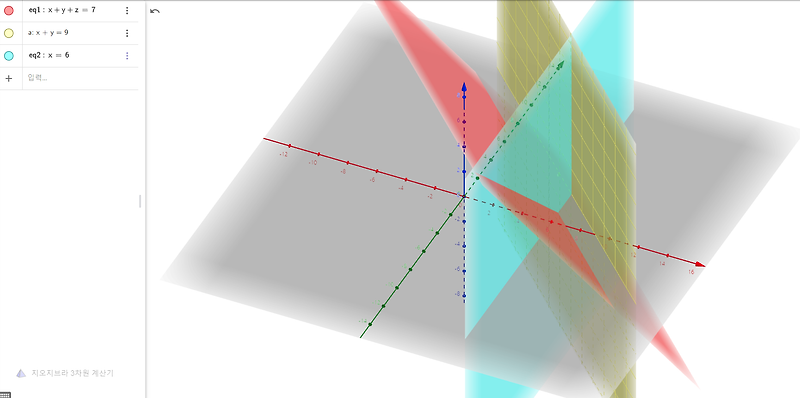
3차원 좌표계에서 평면은 다음과 같은 형태로 표현할 수 있다.
ax + by + cz = d (단, a ≠ 0, b ≠ 0, c ≠ 0)
n차원 좌표계에서의 일차방정식
n개의 변수를 포함하는 일차방정식은 다음과 같이 나타낼 수 있다.
a₁x₁ + a₂x₂ + ... + aₙxₙ = b (단, a₁, a₂, ..., aₙ은 상수이고, b는 0이 아니다.)
위 식에 b에 0을 대입하면 아래와 같은 식이 되는데 이와 같이 상수항이 없는 동차 일차방정식(homogeneous linear equation)이라고 한다.
a₁x₁ + a₂x₂ + ... + aₙxₙ = 0
이러한 동차 일차방정식 여러 개 있는것을 동차 연립방정식(homogeneous system of equation)이라고 부른다.
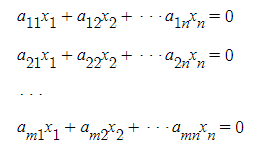
※ 일차방정식은 변수들의 곱이나 제곱근을 포함하지 않는다.
초평면
위에서 배운것처럼 2차원에서는 일차방정식의 그래프가 직선으로 표현되고, 3차원에서는 평면으로 나타난다. 이를 일반화해서 n차원 좌표계에서 생각해보면, 일차방정식은 a₁x₁ + a₂x₂ + ... + aₙxₙ = b형태로 쓸 수 있다. 이 방정식의 그래프는 n차원 공간에서의 초평면(hyperplane)이 된다.
초평면은 평면을 뛰어넘은 평면이라는 뜻인데 수학자들은 '평면'을 일반화하여 '초평면'이라고 부르기로 정의하였다. 일차식으로 만들어지는 도형을 전부 초평면으로 부르기로 한 것인데 각 초평면은 그려진 차원을 이용하여 00차원의 초평면이라고 부른다.
직선은 2차원의 초평면이고, 평면은 3차원의 초평면이다.
2차원에 그려진 초평면 = 직선 = 1차원 공간
3차원에 그려진 초평면 = 평면 = 2차원 공간
위의 수식을 보면 알겠지만 초평면은 초평면이 그려지는 차원보다 한차원 낮은 공간이다.
초평면은 공간을 분할하는 역할을 한다. 2차원 평면의 초평면은 직선이고 직선은 평면을 분할한다. 3차원 공간의 초평면은 평면이고 평면은 공간을 분할한다. 차원이 높아지면 상상할 수는 없지만, 같은 원리가 성립한다는 것은 이해할 수 있다. n차원의 초평면은 n차원 공간을 분할할 것이다.
이 원리는 머신러닝에서 데이터를 분류하는 모델을 만들 때 사용된다.
참고자료
[2] 티스토리 - 수학의 본질
'🔣 Math > Linear Algebra' 카테고리의 다른 글
| [선형대수학] 2.연립일차방정식, 확대행렬 (0) | 2024.09.25 |
|---|
