확률과 통계의 관계
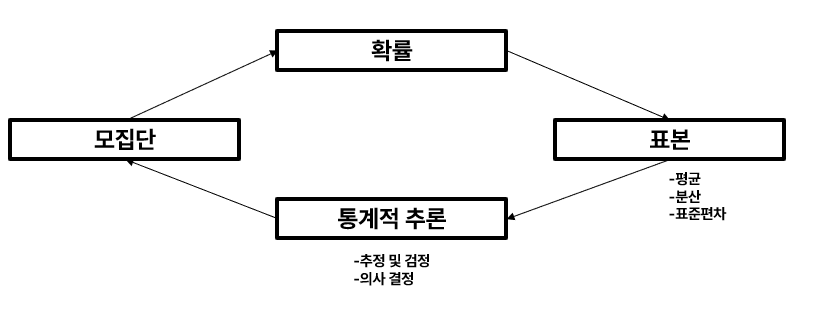
확률과 통계는 서로 독립적인 학문이다. 하지만 통계를 제대로 이해하려면 확률에 대한 지식이 필수적이다. 즉, 확률을 공부할 때 통계의 세부 사항을 몰라도 괜찮지만, 통계를 배우려면 확률 개념을 이해해야 한다. 아래 그림은 확률과 통계의 관계를 직관적으로 보여줄 수 있다.
표본공간(Sample Space)
확률 이론은 표본공간(sample space)의 정의부터 시작한다. 표본공간은 실험의 결과 하나하나를 모두 모은 것을 뜻하며 S로 표기된다.

예를 들어, 두 개의 동전을 던졌을 때 앞면과 뒷면이 나오는 표본공간은 다음과 같다.
S = {앞앞, 앞뒤, 뒤앞, 뒤뒤}
세 개의 동전을 던지는 경우의 표본공간은 다음과 같이 표현할 수 있다.
S = {앞앞앞, 앞앞뒤, 앞뒤앞, 뒤앞앞, 앞뒤뒤, 뒤앞뒤, 뒤뒤앞, 뒤뒤뒤}
중심이 원점이고 반지름이 3인 원의 표본공간은 다음과 같이 표현된다.
S = {(x, y) | x² + y² ≤ 9}
사건(events)
이렇게 표본공간은 가능한 모든 결과를 나타내기 때문에, 이 결과들을 가지고 부분집합을 만들 수 있다. 이 부분집합을 사건(events)이라고 부른다.
어떤 제품 중에서 3개를 추출하여 검사한 후 정품과 불량품으로 구분할 때, 불량품의 개수가 1개 이상인 사건을 구하려면 먼저 표본공간을 알아야 한다.
정품을 T, 불량품을 F라고 하면, 표본공간 S는 다음과 같다.
S = {TTT, TTF, TFT, FTT, TFF, FTF, FFT, FFF}
여기서 불량품 개수가 1개 이상인 사건 A는 다음과 같이 정의할 수 있다.
사건 A = {TTF, TFT, FTT, TFF, FTF, FFT, FFF}
여기서 알 수 있는 점은 사건은 표본공간 밖에서 만들어질 수 없다는 것이다. 사건은 표본공간의 부분집합이기 때문이다.
참고자료
'🔣 Math > Probability' 카테고리의 다른 글
| [확률론] 2.사건(Events) (1) | 2024.09.13 |
|---|---|
| Combinatorial Analysis(조합분석) (0) | 2024.08.19 |
